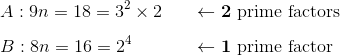This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!
6.9: Prime Factors
Another page, another great plug-in opportunity. For any given n, it will only take us a few steps to evaluate Quantities A and B. Moreover, plugging in even one value for n will allow us to clear away two of the four answers. At that point, even if we run out of time and have to guess, we’ve doubled our chance of getting the problem right.
First, just to clear up a possible misconception: different prime factors means no duplicates are allowed. The prime factorization of 60 is
so 60 has 3 different prime factors: 2, 3, and 5.
Let’s try out some different values of n. First, let n = 1, the smallest integer allowed by the problem:
When n = 1, the number of different prime factors of 9n (Qty. A) is equal to the number of different prime factors of 8n (Qty. B). This means we can rule out answers (A) and (B).
For our next plug-in, let’s try n = 2.
This time, Qty. A (number of different prime factors of 9n) is greater than Qty. B (number of different prime factors of 8n). Because the quantities are sometimes equal, and sometimes unequal, we choose answer (D) for “depends on the variable.”
Math Review Reference
For more on this topic, see the following section of the GRE Math Review:
- 1.1: Integers (pp. 1-2)