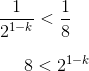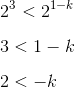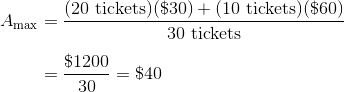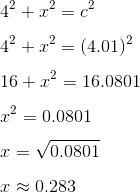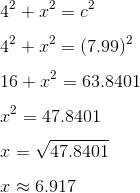This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!
5.24: Rangefinding with Triangles
Right away we can see that this question is a bit different from the standard multiple choice that predominates on the GRE. As with the “triple true-false” problems (e.g., 5.15 and 5.18), there may be multiple correct answers, and we have to find them all. But 5.24 has twice as many answers as those earlier problems, creating the possibility of a huge time sink. On the plus side, the answers are arranged in increasing numerical order, potentially simplifying our task.
This setup, which I call a rangefinding problem, isn’t specific to geometry questions. It occurs across all four content areas: 6.25 is an arithmetic example, and ETS materials from previous years have featured algebra and statistics-themed ones as well. This should motivate us to look for a general approach that works well, so that we can apply it to any rangefinding problem — whether it’s about parallelograms, π, or probability.
Let’s start with what not to do: plug in the answers one-by-one and check to see if they’re valid. Taking that approach in this problem would mean cranking through at least six applications of the Pythagorean theorem. Individually, these are fairly simple calculations, but if you do them half a dozen times, the minutes start to ebb away.
Instead, we can try the following:
- Find (or approximate) the minimum value of x that satisfies the problem conditions.
- Find (or approximate) the maximum value of x that satisfies the problem conditions.
- Select all the answers in between those two endpoints.
This way, we only need to calculate twice — once to find the min, and once to find the max. With six answers, this cuts our work down to 1/3. Some problems of this type have 7 or even 8 answers; in those cases, the time savings from this method are even greater.
Find the Min
Now, how do we find the smallest possible value of x? The length of one leg (AB) is fixed, so in order to decrease x (the length of leg BC), we need to shorten the hypotenuse (AC). If we call the hypotenuse length c, the following equation (which is just Pythagoras with substitutions) will give us our value for x:
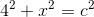
When the hypotenuse is at its shortest, x will be small. So how short can the hypotenuse get? Well, the problem stem tells us that the length must be between 4 and 8, and on the GRE, between means strictly between: the endpoints of the interval are not included. Thus, the hypotenuse length is described by the following inequality.
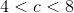
The upshot is that we can’t just set c equal to 4, as convenient as that would be for our calculations. We can, however, choose something arbitrarily close to 4, but slightly larger.
Let c = 4.01. Then
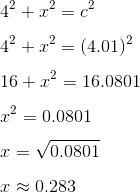
This is not the least possible value of x, but it’s sufficient for our purposes because it’s smaller than any of the answer choices. In other words, no answer choice can be excluded for being too small, because we can construct a triangle whose x is even smaller.
Find the Max
The same logic applies to finding the greatest value of x. If we maximize c (within the bounds provided by the problem), we also maximize x. Remember that we can’t set c equal to 8, but we can get as close as we like.
Let c = 7.99. Then
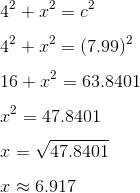
Again, this is only an approximation of the upper bound for x. (If we set c equal to 7.999, or 7.9999 we’d get closer still to the true maximum.) But it serves its purpose, which is to show that none of the answer choices are too large to be a possible value of x.
At this point, we’ve shown that x can be any number between 0.283 and 6.917. That range includes all six answers, so the correct response is “all of the above” or (ABCDEF).
Notice, by the way, that this is another geometry problem which we solved without diagramming (cf. 5.7). In this case, drawing the triangle might even be counterproductive, since a diagram necessarily involves some assumptions about what the shape is supposed to look like. Once you’ve drawn a shape a certain way, it’s hard to “unsee” that particular interpretation of the data.
Math Review Reference
For more on this topic, see the following section of the GRE Math Review:
- 3.3: Triangles (pp. 48-49)