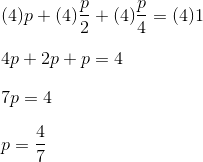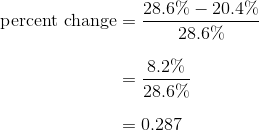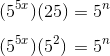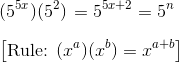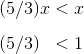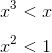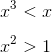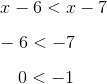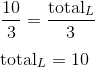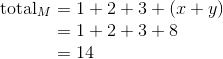This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!
5.15: An Inequality Ready Check
This problem is designed to test your comfort level in manipulating inequalities. When they hand you a problem like this, the testmakers are checking to see if you know one rule in particular:
When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality reverses.
As a little warm-up, consider the inequality
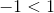
If we multiply both sides by (-1), we have to reverse the sign, or the statement won’t make sense anymore:
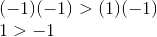
This is important in problem 5.15 because it asks us to consider both positive and negative values of x. We can simplify our task by considering the positive values first, but ultimately we’ll need to deal with the negatives as well. Let’s step through the answer choices one at a time.
Answer Choice A
Let x be any positive number. Then we can divide out the x from both sides as follows:
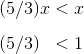
But this is a contradiction, because 5/3 is actually greater than 1. Since assuming that x is positive leads to an incorrect result, we can conclude that inequality (A) has no positive solution. Answer choice (A) is therefore incorrect.
Answer Choice B
Again, we begin by assuming x is positive and dividing out an x to simplify the expression:
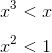
Because x is positive, taking the square root of both sides gives us
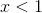
In other words, inequality (B) is true for any positive x less than 1. So answer choice (B) passes our first test. Now what about negative values of x?
Let’s go back to the original inequality, this time assuming that x < 0. Under this new assumption, if we divide out an x from both sides, we have to flip the sign of the inequality.
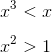
This time around, we don’t even have to take the square root: almost any negative value of x is a solution. (Try x = -2, for example, or x = -10.) Because we can find both positive and negative solutions for the inequality, answer choice (B) is a keeper.
Answer Choice C
That leaves us with one final option to evaluate. This one’s actually a little simpler, because we can subtract out the x rather than dividing or multiplying. When you add or subtract a number from both sides of an inequality, it doesn’t change the sign. Thus, we don’t have to decide in advance whether x is negative or positive.
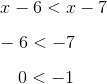
Indeed, it doesn’t end up mattering whether x is negative, positive, or even zero. As shown above, any real value of x leads to a contradiction, meaning that inequality (C) has no real solution at all. We can therefore reject answer (C), leaving (B) as the only correct answer.
A Note on Time Management
As you may have noticed, 5.15 is more time-consuming than most of the other math problems we’ve encountered so far. That’s largely because it requires you to test out a bunch of different cases and see which ones are valid. In other problems, like 5.11 and 5.13, you set up a single equation and solve for a single variable, but in this problem, it’s imperative that you test out each of the answer choices. Even if algebra is your strong suit, “case-by-case” problems like 5.15 may be worth skipping on your first pass through the section. That way, you’ll be sure not to miss any of the faster, easier problems that might appear later on.
Math Review Reference
For more on this topic, see the following section of the GRE Math Review:
- 2.5: Solving Linear Inequalities (pp. 23-24)