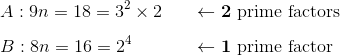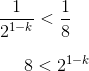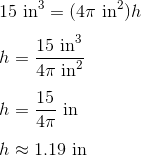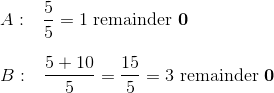This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.15: Counting Integers

This problem is an illustration of the multiplication principle (also known as the rule of product), which states:

If you have two independent choices to make, one with x different possibilities and another with y different possibilities, then there are xy possible pairs to choose from.

If you have 5 choices of entrée and 3 choices of dessert on a dinner menu, then you have 15 possible choices for your meal. Similarly, if you choose one of 7 ice cream flavors and one of 4 toppings, then you have 28 possible arrangements to choose from. (For some mysterious yet delightful reason, all of the classic examples of this principle involve food.)

In this problem, we apply the multiplication principle by

• figuring out how many possibilities there are for the tens digit (x)
• figuring out how many possibilities there are for the units digit (y)
• multiplying together x and y to get the overall number of possibilities

The tens digit, we’re told, must be greater than 6. Given that restriction, there are 3 possibilities:

{7, 8, 9}

The units digit has to be less than 4, which leaves us with 4 possibilities (don’t forget zero!):

{0, 1, 2, 3}

3 possibilities for the tens digit and 4 for the units digit makes

which corresponds to answer (D). Specifically, the possible integers are

{70, 71, 72, 73, 80, 81, 82, 83, 90, 91, 92, 93}

but you clearly don’t need to list the possibilities to get the problem right. In fact, other problems of this type may make it impractical to enumerate the possibilities directly, which is why (apart from saving time) the multiplication principle is so important. (Consider what this problem would be like if it asked about four-digit integers: listing out all of the valid numbers would be extremely unwieldy and time-consuming, but the multiplication principle would still work just fine.)

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 4.3: Counting Methods (p. 75)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.14: Area of a Triangle

This is a little more abstract than the usual GRE triangle problems (e.g., 5.24), but it isn’t any more complicated. All we need to do is recall the triangle area formula:

and replace b with 2h:

Then, we simplify (by combining like terms) to get:

which corresponds to answer choice (C).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 3.3: Triangles (pp. 47-49)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.13: Property Tax

This is another percent-difference problem, similar to 5.19.  Last time, just to refresh your memory, we described the situation in terms of percent change, even though it was actually two different types of taxes we were comparing. Here’s the formula we used.

We can take a similar approach here. Because we’re asked to find our answer in terms of Patricia’s property tax, her tax will be the base, or denominator, in our calculations. The “change” will be the difference between Patricia’s and Steve’s respective property taxes. We’ll call Patricia’s tax P and Steve’s tax S.

But before we can plug those figures into the formula, we need to figure out the value of P. We know S and we know the difference between the two, so we can use those two values together to solve for P:

Now we just plug in P as our denominator, and the difference P – S (which we already know is $140) as our numerator:

Steve’s property tax is about 6.7 percent less than Patricia’s, so the answer is (A).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.7: Percent (pp. 9-12)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.12: The Midpoint Formula

The GRE Math Review doesn’t actually discuss the midpoint formula, but it’s a fundamental coordinate-geometry fact and ought to be committed to memory. You may not need it to get a problem right on the GRE, but knowing it will certainly save you some time if you encounter a question like 6.12.

Here’s the standard form of the formula:

And here’s a prose translation:

To find the midpoint M of two points on an xy-plane, we take the averages, respectively, of the x– and y– coordinates. The x-coordinate of M is the average of the x-coordinates; the y-coordinate of M is the average of the y-coordinates. 

To find the midpoint of R and S, let R be point 1 and S be point 2. Then:

which corresponds to answer choice (C).

Note that this is yet another coordinate-geometry problem we solved without diagramming. I probably seem like I’m harping on this point, but I’ve had more than one student approach this problem by methodically sketching out a pair of xy-axes, then locating R and S on the coordinate plane. This kind of detail is fine if you’re submitting homework for a persnickety TA, but it’s counterproductive on the GRE, where time is of the essence.

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 2.8: Coordinate Geometry (pp. 30-32)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.11: Convention Goers

The theme of this problem is “percentages of percentages.” We could use a table as in problems 5.9 and 5.21, but that’s overkill here, because the problem is so direct. If 32% of the convention goers came from Asia, and 45% of that subgroup are women, then women from Asia constitute

of the overall group of convention-goers. That’s all there is to it, but don’t worry: we’ll get more practice with percentages in problem 6.13.

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.7: Percent (pp. 9-12)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.10: Dueling Copiers

This is a special kind of algebra problem called a work-rate problem. There is a basic procedure for these that we can follow every time. It boils down to two steps:

• Figure out the work rate of each machine (worker, factory, etc.).
• Apply those rates to solve for the target quantity.

In this problem, we have enough information to calculate each machine’s work rate directly:

What we really want to know, however, is the difference in the output of the two machines if each one runs for a specified amount of time:

So we plug in the times (which the problem provides) along with the rates we calculated:

The difference in output is

so the correct answer is (B).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 2.7: Applications (pp. 25-27, see esp. Example 2.7.4)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.9: Prime Factors

Another page, another great plug-in opportunity. For any given n, it will only take us a few steps to evaluate Quantities A and B. Moreover, plugging in even one value for n will allow us to clear away two of the four answers. At that point, even if we run out of time and have to guess, we’ve doubled our chance of getting the problem right.

First, just to clear up a possible misconception: different prime factors means no duplicates are allowed. The prime factorization of 60 is

so 60 has 3 different prime factors: 2, 3, and 5.

Let’s try out some different values of n. First, let n = 1, the smallest integer allowed by the problem:

When n = 1, the number of different prime factors of 9n (Qty. A) is equal to the number of different prime factors of 8n (Qty. B). This means we can rule out answers (A) and (B).

For our next plug-in, let’s try n = 2.

This time, Qty. A (number of different prime factors of 9n) is greater than Qty. B (number of different prime factors of 8n). Because the quantities are sometimes equal, and sometimes unequal, we choose answer (D) for “depends on the variable.”

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.1: Integers (pp. 1-2)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.8: Exponents in the Denominator

This problem combines three mathematical concepts that, by themselves, tend not to cause much trouble: fractions, exponents, and inequalities. If your algebra is a bit shaky, it may help to think of this problem in terms of three basic steps:

• Get rid of the fractions, leaving 2^1-k on one side of the expression.
• Get rid of the exponents, leaving (1 – k) on one side of the expression.
• Solve for k.

To clear out those fractions, we can cross-multiply:

(Note that even though k might end up being negative, 2^1-k will be positive for any real value of k, so we don’t have to worry about sign-flipping here.)

8 is a power of 2, so we can rewrite it as 2³:

Now, remember the property of equality of exponential functions (see problem 5.16 for a refresher)? A similar property applies to inequalities, although the Math Review doesn’t mention it:

The main difference between this and the equality property is that here, the base x has to be greater than 1. Our base in this problem is 2, so we’re in the clear.

For the last step, we multiply both sides by -1 (this time, the direction of the inequality does change).

Because k (Quantity A) is less than -2 (Quantity B), the correct answer is (B).

Math Review Reference

For more on this topic, see the following sections of the GRE Math Review:

• 1.2: Fractions (pp. 3-4)
• 2.2: Rules of Exponents (pp. 18-20)
• 2.5: Solving Linear Inequalities (pp. 23-24)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.7: Height of a Cylinder

Only two kinds of solids (three-dimensional figures) are discussed in the GRE Math Review: rectangular solids (also known as right rectangular prisms) and right circular cylinders, which are your regular “soup can” cylinder with one base directly above the other. (A few more solids are mentioned in passing, but none of their properties are covered in the Review.)

3D geometry questions on the GRE tend to focus on two properties of solids: their surface area and their volume. For both rectangular solids and cylinders, these properties are described by simple formulas. It’s best to memorize these, so you don’t have to reinvent the wheel (or the box, or the can) on test day.

The volume of a right circular cylinder is given by the following equation:

• V is the volume of the cylinder
• r is the radius of the circular bases
• h is the height of the cylinder

If we know two of these quantities, the formula allows us to find the other. Here, we have the radius and the volume, so we can plug those into the formula for a start:

Sanity check: Remember to include the units in your calculations. This way, mistakes will be easier to catch. If we know we’re looking for height, and we get an answer in cubic inches, we know there’s been an error somewhere along the way.

From here we can solve for h in just a few steps:

Because the height (Qty. A) is less than 2 inches (Qty. B), the answer is (B).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 3.6: Three-Dimensional Figures (p. 56)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.6: Division with Remainders

This problem is a great candidate for plugging in: once we decide on a value for n, the arithmetic is pretty simple. Without a concrete example, though, it might be hard to see the pattern that relates the two quantities.

Let’s try n = 5.

The remainders are in bold, just to emphasize the fact that this is what we’re comparing. In this case, Qty. A and Qty. B both equal 0. We can now rule out answers (A) and (B), because the two quantities are equal at least some of the time.

Now, how about n = 8?

Again, the remainders are equal. Once we’ve gotten the same result twice on a Quantitative Comparison, it’s time to step back and look for patterns. There are three basic possibilities here:

• It’s just a coincidence that the remainders were equal both times. (Unlikely!)
• There’s something about the numbers we chose — some shared property — that made the remainders equal. (Possible!)
• There something about the structure of the problem that guarantees that the remainders will be equal, no matter what n we choose. (Possible!)

In this case, the last option is correct. There’s nothing special about the n we chose; any positive integer would give the same results. Because 10 is divisible by 5, adding it to the numerator will never change the remainder. Imagine a clock with just 5 hours on it. In this illustration, it’s 1:00 right now:

But if we advance the time by 10 hours, to 11:00, the clock will look exactly the same, because we’ve gone around the clock exactly twice.

Our answer, by the way, is (C).

(Challenge question: how would the problem be different if we were comparing the remainders of n and (n + 11)? What values of n could we try to demonstrate this behavior?)

A Quick Note about Remainders

Just to clear up a point that some students find confusing: if your dividend is smaller than your divisor, the remainder is the entire dividend — not zero, and not undefined. So if we’d chosen 4 as our value for n above, we’d have gotten the following result.

If this seems counterintuitive, think of it this way: You have a bunch of friends over for dinner and plan to serve cheesecake after the meal. There are 6 people at the table, including yourself, and the cheesecake, which was store-bought, came pre-sliced into 6 neat slices. So the plan is for each person to get 6/6 = 1 slice of cheesecake, with none left over (i.e., no remainder).

But your roommate/spouse/pet, who was not aware of your plans for the cheesecake, has already eaten 2 of the slices. So when you go to the fridge to retrieve the dessert, you find that you have only 4 slices left. It’s a nice evening, so you quickly formulate a backup plan: “Let’s all go out for ice cream!” None of the cheesecake has been divided up among you and your guests, but those four slices are still there in the fridge for later. In other words,

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.1: Integers (pp. 1-2)