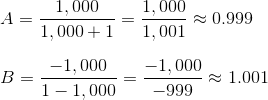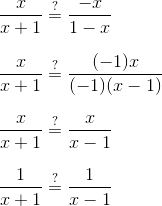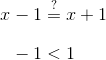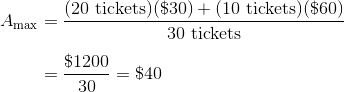This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.5: The One with the Lists

Statistically speaking, this isn’t the hardest math problem in the book — that dubious honor goes to 6.25, which only 24% of students get right. Still, 6.5 deserves a special mention, because its weird wording causes students to spend huge amounts of time just figuring out what’s being asked. It’s true that almost half of students (48%) eventually get this one right, which is a higher success rate than several of the problems we’ve seen so far. Based on my own teaching experiences, though, I have to wonder how many students guess the right answer out of frustration, rather than because they’re confident that it’s correct.

The first thing we have to establish is that T doesn’t have to be a uniform list. As long as all of the numbers in T are different from one another, and all of them are between 0 and 50, that part of the problem statement is satisfied. So T could be uniform, in the sense that there’s a regular interval between each two consecutive values:

But it doesn’t have to be. We could just as easily have something like this:

where there’s a huge jump between consecutive values. There may even be more than one such jump. As long as the smallest value is greater than 0, and the largest value is less than 50, all bets are off.

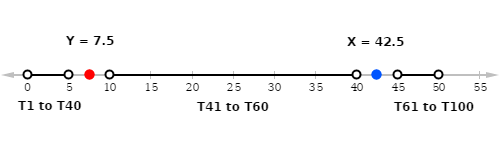
The next thing is to get clear on the definitions of x and y. The problem defines x as “greater than 60 percent” of the values in T. There are exactly 100 values in T, so being greater than 60 percent of those values means being greater than 60 of those values. In other words, if we arrange all of the elements of T in numerical order — call them T₁ through T₁₀₀ — x will be greater than T₆₀ and less than T₆₁. Likewise, y has to be greater than T₄₀ but less than T₄₁.

In a sense, this is a problem with 100 independent variables, {T₁ … T₁₀₀}, and two dependent variables (x and y). That fact alone should make us suspect that the answer will be (D). This is where most of that 48% gets off the bus.

But let’s see if we can come up with some scenarios in which (x – y) is less than, greater than, or equal to 20. If we can show that at least two of those outcomes are possible, we can select answer (D) with confidence.

Actually, both of the example lists above will result in (x – y) being less than 20. So will most of the “common-sense” approaches to making a list like T. Our real challenge here is figuring out a situation in which x – y ≥ 20.

Here’s the thing, though: we don’t need to create an entire list T, and we certainly don’t need to write it out element-by-element. All we really care about are the following properties:

• All of the numbers before y are small.
• All of the numbers after x are large.
• Somewhere between y and x, there’s a big jump in values.

The number line below shows one of the many (actually, infinite) ways to accomplish this.

All of the numbers before y (T1 to T40) are less than 5, and all of the numbers after x (T61 to T100) are greater than 45. In between, there’s a huge space for the numbers from T41 to T60. If we arrange the elements of T in this way, we create a big gap between y and x, making x – y much greater than 20.

At this point, we’ve shown that (x – y) can be greater or less than 20, depending on the way that we populate list T. The answer is therefore (D), as in “depends on the variables.”

Now, if you get a problem like this on the real exam, I don’t recommend actually drawing out a number line, or even constructing a list like T. Instead, reason informally about how you might manipulate the independent variables (here, the values in T) in order to minimize, and then maximize, the dependent variables.

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.5: Real Numbers (pp. 7-8)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.4: To Define a Line

This problem hinges on a basic question about coordinate geometry:

What information is needed to define a line on the xy-plane?

More specifically, we want to know:

Do we have enough information to define lines j and k, and thus to determine the slopes of the two lines?

As is often the case in Quantitative Comparison questions, we’ll need to be careful to separate inferences from assumptions. We may or may not be able to infer the slopes of the two lines from the information provided; if we can’t, we have the option of choosing (D) for “don’t know.” But we have to avoid assuming anything extra that isn’t supported by the problem statement.

Once you recognize what the problem is really asking, you may find that you can answer it without drawing a diagram. If you do diagram, proceed with caution! For many students, the first instinct is to sketch something like this:

where both lines pass through the origin. In this case, the slope of line j is clearly greater than the slope of line k (specifically, m_j = 2 and m_k = 1/2). But the problem stem doesn’t tell us that the lines pass through the origin: all it says is that j passes through (1,2) and k passes through (2,1). Consequently, the above graph is only one possible interpretation of the problem. We can’t conclude that m_j > m_k on the basis of this drawing alone.

In fact, it’s also possible to draw lines j and k parallel, while still obeying all of the constraints supplied by the problem:

(Here, m_j = m_k =1/2.)

We could even, if we wanted to, draw the two lines in such a way that m_j < m_k:

As you probably suspect by now, we simply don’t have enough information to determine the slopes of lines j and k, which means our answer must be (D). This is because we need two points to define a line, and the problem only gives us one point for each line. If the problem gave us just a little more information (say, that both lines really do pass through the origin), it would be a different story altogether.

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 2.8: Coordinate Geometry (pp. 30-32)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.3: Fractions, Two Ways

This problem, with its single, loosely defined variable x, is an excellent illustration of the flexibility we have on Quantitative Comparison questions. We can solve this one either by plugging in a couple times and reasoning about the result, or by simplifying the expression algebraically until one quantity is clearly larger than the other. The two methods take about the same amount of time, and my classroom students are about 50/50 as to which method they find easier.

The Plug-In Approach

We can set x equal to any value greater than 1, but integers will be the easiest to work with. Unless there’s a compelling reason to try improper fractions or decimals, we’ll stick with integer plug-ins in general.

First, let’s try x = 2, the smallest allowable integer value:

In this case, B is greater. At this point we can rule out answer choices (A) and (C), because we now have a counterexample to show that

• At least some of the time, Quantity A is not greater than Quantity B.
• At least some of the time, the two quantities are not equal.

(We only select answer choice (A) if Qty. A is always greater than Qty. B, under all conditions permitted by the problem statement. Likewise, we only select (C) if the quantities are always equal.)

Now let’s try a huge number, just to see if that makes a difference. Let x = 1,000:

Quantity B is still greater. In fact, no matter how high we set x, Qty. B is going to be at least a little bit larger than 1, because its denominator will always be smaller than its numerator. Likewise, Qty. A will always be smaller than 1, because its denominator is always larger than its numerator. Both quantities approach 1 as x increases, but neither actually makes it to the border. The correct answer is (B).

The Algebraic Approach

Now let’s rewind and tackle the problem algebraically. We can think of the comparison as a mathematical relationship — an equation or inequality whose direction, if any, just hasn’t been determined yet:

We can manipulate this mystery relationship the same ways we’d manipulate an equation or inequality, such as

• adding a term to both sides
• subtracting a term from both sides
• multiplying both sides by the same factor
• dividing both sides by the same divisor

The only caveat is that we ought to avoid multiplying or dividing by negative numbers, since those would require us to flip the sign of this “maybe-equation, maybe-inequality.” (It’s not mathematically invalid to do this, but the bookkeeping gets unnecessarily complicated.) Fortunately, x is defined as a positive number, so we won’t need to worry about this for the current problem.

Our goal now is to simplify the two expressions until it’s clear which one, if either, corresponds to the greater quantity.

At this point, it may already be evident that the quantity on the right has to be greater: it has the same numerator as the quantity on the left, but a smaller denominator. If that’s not entirely clear, we can cross-multiply to simplify the expressions even further:

The quantity on the right turns out to be greater regardless of what x we choose, so answer choice (B) is our winner.

Math Review Reference

For more on this topic, see the following sections of the GRE Math Review:

• 1.2: Fractions (pp. 3-4)
• 2.5: Solving Linear Inequalities (pp. 23-24)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.2: Theater Tickets

This problem is similar to the rangefinding exercise we saw in the last section (5.24). Instead of unsystematically trying out different combinations of ticket prices, the best approach here is to focus on the minimum and maximum values for quantity A. More specifically, we want to determine whether A_min and A_max are greater than, less than, or exactly equal to $50.

Let’s start with A_min, the lowest possible average ticket price. Without even calculating anything, we can see that this minimum price has to be less than $50 — if all of the individual tickets sell for less than $50, the average price has to be less than $50 as well. (If this isn’t quite clear, think of it this way: if nobody gets an A in a class, then the class average can’t be an A.)

How about the maximum average ticket price (A_max)? We can set an upper bound by just assuming that all of the tickets sell for their maximum individual price:

Remember that in the language of GRE math, between means strictly between, so this is actually a slight overestimate. The maximum allowable ticket prices would actually be something like $29.99 and $59.99, respectively. Either way, the average price is less than $50, even if all of the tickets are sold for the highest possible price.

Since the highest possible average price (Quantity A) is still less than $50 (Quantity B), our correct answer is (B).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 4.2: Numerical Methods for Describing Data (pp. 68-69)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.1: Two Equilateral Triangles

This isn’t a trick question, exactly, but it’s close. You might think from the problem stem that you’ll be comparing the triangles to each other, since they tell you (in a roundabout way) that triangle T is bigger than triangle X. But the relative sizes of T and X actually end up being irrelevant to the solution — a classic “TMI” (too much information) scenario. More than anything else, this problem is an object lesson in the importance of reading carefully, even when you’re 3 hours into the exam.

Quantity A: Because T is an equilateral triangle, all of its sides are congruent. The ratio of its side lengths (Qty. A) is therefore 1:1 = 1.

Quantity B: Likewise, X is an equilateral triangle, so its sides are all congruent to each other. The ratio of the lengths of any two of those sides (Qty. B) is also 1:1 = 1.

Quantities A and B are equal, so the answer to this Quantitative Comparison is (C), as in “See, they’re the same!”

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 3.3: Triangles (pp. 47-48)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.25: Fixed and Variable Costs

This problem invokes a situation that is not explicitly mentioned in the GRE Math Review, but is important enough to merit its own formula:

Unlike the simple interest formula (see 5.13), which should be memorized, the total cost formula does not come into play frequently enough that you have to memorize it. As long as you understand the difference between fixed and variable costs, and how to account for each, you can skip straight to the application without writing down “T = F + V” or any such expression.

The variable costs, in this problem, consist of two parts: the number of units produced and the rate per unit. Substituting that into our initial formula gives

This expression that will serve as our template for solving the problem. Reading through the problem stem, we see that our target value is the fixed cost — which, true to its name, does not change from month to month. In order to find that value, we will first need to determine the variable cost and subtract it out from the totals provided for each month. Here’s what we know at the start of the problem:

We can use that information to populate two equations: one for each month.

Subtracting one equation from the other allows us to figure out the unit cost:

Once we have our unit cost, we can plug it back into the equation for either month and use it to determine the fixed cost:

Here, I’ve used the first equation (from the 20,000-unit month), but using the second equation (the month with 25,000 units) gives the same result. Either way, the correct answer is $30,000 (B).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 2.7: Applications (pp. 25-28)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.24: Rangefinding with Triangles

Right away we can see that this question is a bit different from the standard multiple choice that predominates on the GRE. As with the “triple true-false” problems (e.g., 5.15 and 5.18), there may be multiple correct answers, and we have to find them all. But 5.24 has twice as many answers as those earlier problems, creating the possibility of a huge time sink. On the plus side, the answers are arranged in increasing numerical order, potentially simplifying our task.

This setup, which I call a rangefinding problem, isn’t specific to geometry questions. It occurs across all four content areas: 6.25 is an arithmetic example, and ETS materials from previous years have featured algebra and statistics-themed ones as well. This should motivate us to look for a general approach that works well, so that we can apply it to any rangefinding problem — whether it’s about parallelograms, π, or probability.

Let’s start with what not to do: plug in the answers one-by-one and check to see if they’re valid. Taking that approach in this problem would mean cranking through at least six applications of the Pythagorean theorem. Individually, these are fairly simple calculations, but if you do them half a dozen times, the minutes start to ebb away.

Instead, we can try the following:

• Find (or approximate) the minimum value of x that satisfies the problem conditions.
• Find (or approximate) the maximum value of x that satisfies the problem conditions.
• Select all the answers in between those two endpoints.

This way, we only need to calculate twice — once to find the min, and once to find the max. With six answers, this cuts our work down to 1/3. Some problems of this type have 7 or even 8 answers; in those cases, the time savings from this method are even greater.

Find the Min

Now, how do we find the smallest possible value of x? The length of one leg (AB) is fixed, so in order to decrease x (the length of leg BC), we need to shorten the hypotenuse (AC).  If we call the hypotenuse length c, the following equation (which is just Pythagoras with substitutions) will give us our value for x:

When the hypotenuse is at its shortest, x will be small. So how short can the hypotenuse get? Well, the problem stem tells us that the length must be between 4 and 8, and on the GRE, between means strictly between: the endpoints of the interval are not included. Thus, the hypotenuse length is described by the following inequality.

The upshot is that we can’t just set c equal to 4, as convenient as that would be for our calculations. We can, however, choose something arbitrarily close to 4, but slightly larger.

Let c = 4.01. Then

This is not the least possible value of x, but it’s sufficient for our purposes because it’s smaller than any of the answer choices. In other words, no answer choice can be excluded for being too small, because we can construct a triangle whose x is even smaller.

Find the Max

The same logic applies to finding the greatest value of x. If we maximize c (within the bounds provided by the problem), we also maximize x. Remember that we can’t set c equal to 8, but we can get as close as we like.

Let c = 7.99. Then

Again, this is only an approximation of the upper bound for x. (If we set c equal to 7.999, or 7.9999 we’d get closer still to the true maximum.) But it serves its purpose, which is to show that none of the answer choices are too large to be a possible value of x.

At this point, we’ve shown that x can be any number between 0.283 and 6.917. That range includes all six answers, so the correct response is “all of the above” or (ABCDEF).

Notice, by the way, that this is another geometry problem which we solved without diagramming (cf. 5.7). In this case, drawing the triangle might even be counterproductive, since a diagram necessarily involves some assumptions about what the shape is supposed to look like. Once you’ve drawn a shape a certain way, it’s hard to “unsee” that particular interpretation of the data.

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 3.3: Triangles (pp. 48-49)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.23: A Certain Experiment

Unlike problem 5.9, which was merely “probability-flavored,” this problem actually tests your knowledge of a few basic probability properties. The problem stem gives us two key facts about the outcomes of the experiment:

1. They are collectively exhaustive (at least one of the three must occur).
2. They are mutually exclusive (only one of the three can occur in a given trial).

Because the outcomes are collectively exhaustive, the sum of their probabilities must be at least 1. Because the outcomes are mutually exclusive, the sum of their probabilities can be at most 1. Putting the two together, we arrive at a helpful rule:

If a set of events is both collectively exhaustive and mutually exclusive, the probabilities of the events sum to 1.

In this problem, the rule translates to the following equation:

at which point we’ve reduced a probability problem to an algebra problem. (On the GRE, this is always a step forward.) Now we can solve for p directly:

which corresponds to answer choice (D).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 4.4: Probability (pp. 78-80)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.22: Factors and Divisibility

Divisibility, factoring, and primes are big themes in GRE arithmetic, but the problems vary widely in difficulty. Unlike algebra and geometry, there are few telltale signs to let you know when a factoring problem is going to be hard, time-consuming, or both. The underlying math is usually pretty simple, but you may have to try a bunch of different cases before you eliminate all of the incorrect answers.

Here, we can start by finding a number that is “divisible by both 8 and 15.” Rather than looking around for such a number, we can manufacture one by multiplying the two factors together:

(8)(15) = 120

Now, we need to see if 120 is divisible by each of the integers in the answer list. (We can do this by inspection, or we can break out the on-screen calculator.) “Divisible” means that if we divide 120 by that integer, the quotient will also be an integer.

Of our five potential divisors, only 24 (B) survives the divisibility test.

In a way, we’ve lucked out here: the first product we tried (120) was sufficient to eliminate all of the wrong answers. If you found this problem just a little too easy, consider the following slightly harder variant:

x is an integer divisible by both 28 and 6. x must also be divisible by which of the following five integers?

{8, 12, 16, 24, 36}

If you try to approach this problem using the same method as in 5.22, what happens? Why? What makes the factor pair {28, 6} different from the pair {8, 15}, and what must be done differently as a result?

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.1: Integers (p. 1)

This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.21: Judicial Appointees

This problem has some major similarities to 5.9. Both ask us to reason about a group of people based on a set of overlapping characteristics. Because there are two “dimensions” to this problem (gender and minority status), we can even use the same table setup as in 5.9, where the dimensions were sex and age.

Here’s our initial setup, with the target value represented by bold question marks:

Most of the remaining information is given in terms of percentages or fractions. Just as in 5.9, we need to translate the percentages and fractions into whole numbers, since this is the form our answer will have to take. We begin by considering women and minority groups separately:

• (0.30)(180) = 54 appointees were women
• (0.25)(180) = 45 appointees were from minority groups

Here’s what that looks like in chart form:

The next piece of the puzzle is the overlap between women and minority groups:

• (1/9)(54) = 6 appointees were women from minority groups

Adding that fact to our chart allows us to fill in all of the remaining blanks.

At this point, we can see that 87 of the judicial appointees were neither women nor from minority groups. Therefore, the correct answer is (C).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 4.3: Counting Methods (pp. 73-75)