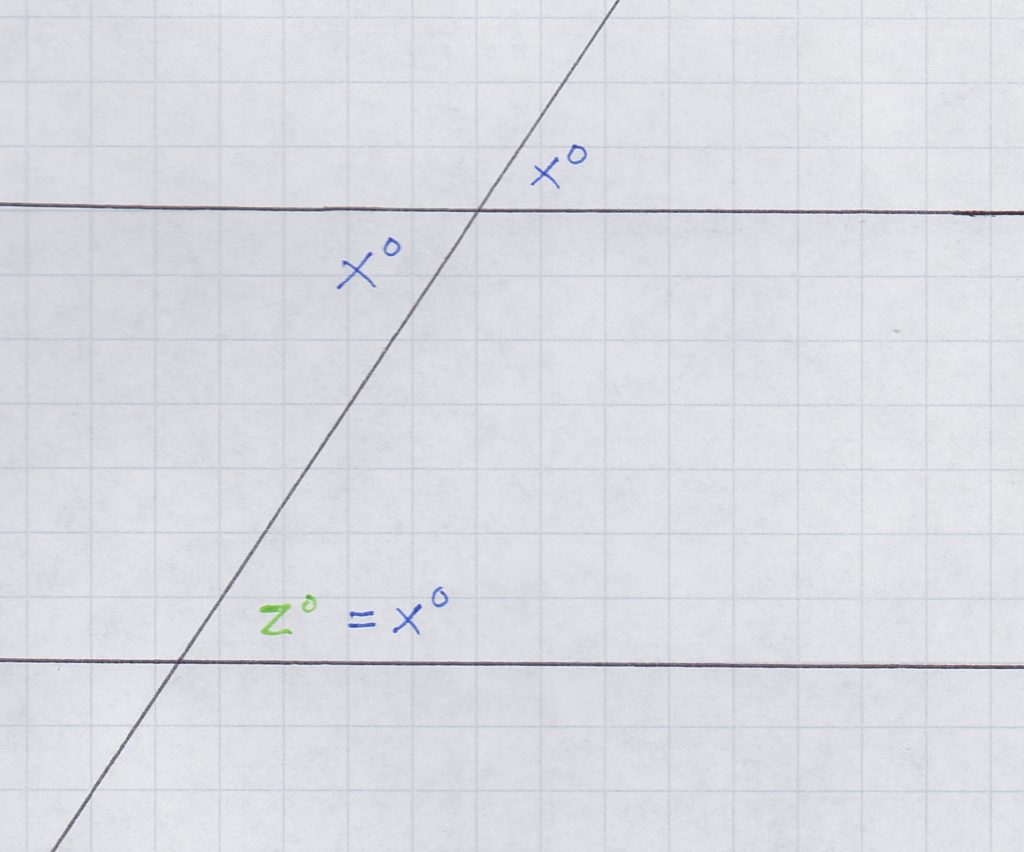This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.1: Transversals and Triangles

Depending on how much you like geometry, this first problem could be nerve-wracking or reassuring. Triangles are hands-down the GRE’s most favorite shape, so it behooves you to get comfortable with them if you aren’t already. There are at least two approaches we can use to solve this one.

Method 1: Transversals

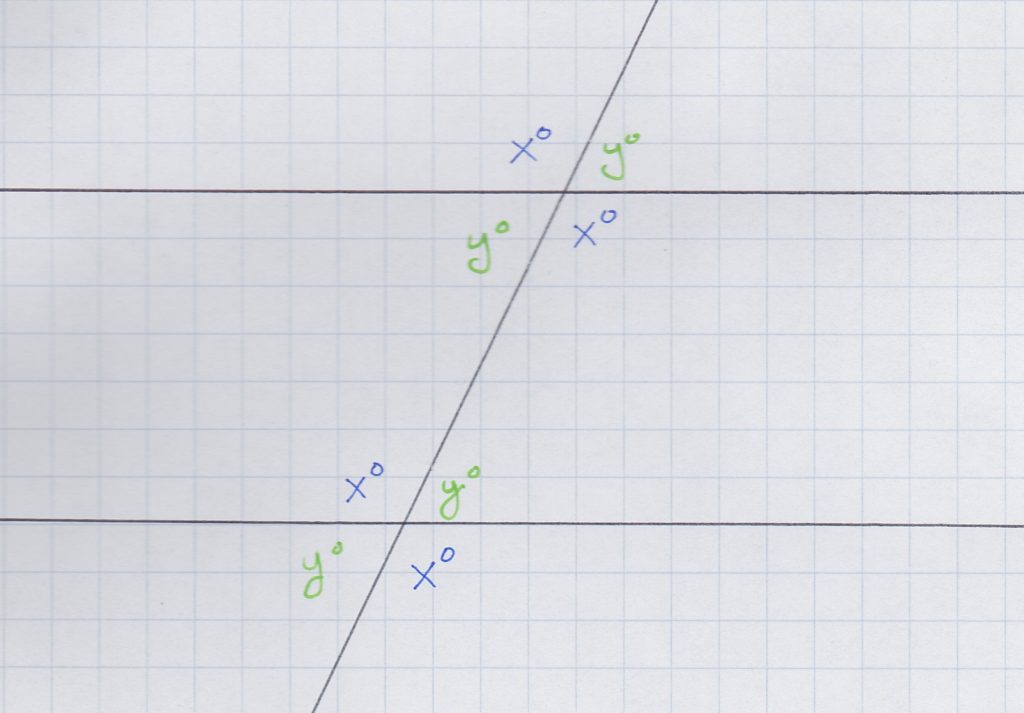
The key to this method is that k and m are parallel. When two parallel lines are intersected by a third line, we wind up with a situation called a transversal of parallel lines. This arrangement has a special property that will help us out: corresponding angles are congruent. This means that for every angle at a given intersection, there is a congruent angle in the corresponding position at the other intersection. Think of it in terms of streets: the “northwest” corner of each intersection is the same. The “southwest” corners also match, and so forth.

Add to this the fact that vertical angles are congruent (this is true for any intersection of two lines), and you get the following:

But how does this fit into the diagram from the problem? Well, let’s forget about angles y and w for a moment and just focus on angles x and z. Imagine extending the left leg of the triangle upward so that it crosses line k, and downward so that it crosses line m. What do we get? A transversal of parallel lines.  The angle that is vertical to x must be congruent to x, and that angle corresponds to z, so all three of these angles must be congruent:

So we’ve shown that x = z. Using the same process, we can also show that angles y and w are congruent. If x = z and y = w, then

x + y = z + w

and the two quantities are equal (answer C).

Method 2: Triangles

The other route of solution depends on that middle angle between x and y. Let’s call it angle t. We know that x + y + t forms a straight angle, which is 180 degrees:

x + y + t = 180

But t is also an interior angle of a triangle, together with angles z and w. These three must also add up to 180:

z + w + t = 180

Because equality is transitive, we can combine the two previous equations to get the following:

x + y + t = z + w + t

Then we subtract t out from both sides to find that

x + y = z + w

which, reassuringly, is the same answer we got with the first method.

Why Two Solutions?

You may wonder why I’m bothering to show multiple methods of solution, when you only need to get the problem right once. With GRE math, it’s always a good idea to have more than one way to solve a problem, in case they surprise you with a variation where one solution method works but the other one doesn’t. In this problem, for example, what if lines k and m weren’t parallel? Method 1 (transversals) wouldn’t work anymore, but Method 2 (triangles) would work just fine.

Math Review Reference

For more on these topics, see the following sections of the GRE Math Review:

• 3.1: Lines and Angles (pp. 45-46)
• 3.3: Triangles (p. 47)