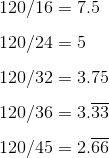This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!

5.22: Factors and Divisibility

Divisibility, factoring, and primes are big themes in GRE arithmetic, but the problems vary widely in difficulty. Unlike algebra and geometry, there are few telltale signs to let you know when a factoring problem is going to be hard, time-consuming, or both. The underlying math is usually pretty simple, but you may have to try a bunch of different cases before you eliminate all of the incorrect answers.

Here, we can start by finding a number that is “divisible by both 8 and 15.” Rather than looking around for such a number, we can manufacture one by multiplying the two factors together:

(8)(15) = 120

Now, we need to see if 120 is divisible by each of the integers in the answer list. (We can do this by inspection, or we can break out the on-screen calculator.) “Divisible” means that if we divide 120 by that integer, the quotient will also be an integer.

Of our five potential divisors, only 24 (B) survives the divisibility test.

In a way, we’ve lucked out here: the first product we tried (120) was sufficient to eliminate all of the wrong answers. If you found this problem just a little too easy, consider the following slightly harder variant:

x is an integer divisible by both 28 and 6. x must also be divisible by which of the following five integers?

{8, 12, 16, 24, 36}

If you try to approach this problem using the same method as in 5.22, what happens? Why? What makes the factor pair {28, 6} different from the pair {8, 15}, and what must be done differently as a result?

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.1: Integers (p. 1)