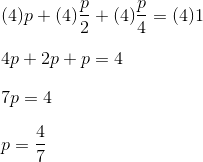This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 5 a shot before reading this!
5.23: A Certain Experiment
Unlike problem 5.9, which was merely “probability-flavored,” this problem actually tests your knowledge of a few basic probability properties. The problem stem gives us two key facts about the outcomes of the experiment:
- They are collectively exhaustive (at least one of the three must occur).
- They are mutually exclusive (only one of the three can occur in a given trial).
Because the outcomes are collectively exhaustive, the sum of their probabilities must be at least 1. Because the outcomes are mutually exclusive, the sum of their probabilities can be at most 1. Putting the two together, we arrive at a helpful rule:
If a set of events is both collectively exhaustive and mutually exclusive, the probabilities of the events sum to 1.
In this problem, the rule translates to the following equation:
at which point we’ve reduced a probability problem to an algebra problem. (On the GRE, this is always a step forward.) Now we can solve for p directly:
which corresponds to answer choice (D).
Math Review Reference
For more on this topic, see the following section of the GRE Math Review:
- 4.4: Probability (pp. 78-80)