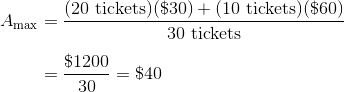This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.2: Theater Tickets

This problem is similar to the rangefinding exercise we saw in the last section (5.24). Instead of unsystematically trying out different combinations of ticket prices, the best approach here is to focus on the minimum and maximum values for quantity A. More specifically, we want to determine whether A_min and A_max are greater than, less than, or exactly equal to $50.

Let’s start with A_min, the lowest possible average ticket price. Without even calculating anything, we can see that this minimum price has to be less than $50 — if all of the individual tickets sell for less than $50, the average price has to be less than $50 as well. (If this isn’t quite clear, think of it this way: if nobody gets an A in a class, then the class average can’t be an A.)

How about the maximum average ticket price (A_max)? We can set an upper bound by just assuming that all of the tickets sell for their maximum individual price:

Remember that in the language of GRE math, between means strictly between, so this is actually a slight overestimate. The maximum allowable ticket prices would actually be something like $29.99 and $59.99, respectively. Either way, the average price is less than $50, even if all of the tickets are sold for the highest possible price.

Since the highest possible average price (Quantity A) is still less than $50 (Quantity B), our correct answer is (B).

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 4.2: Numerical Methods for Describing Data (pp. 68-69)