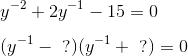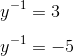This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!
6.24: Quadratics with Negative Exponents
This is another one of those “combo” problems, where the GRE tests you on two topics at once. You may recognize from the setup that this is a quadratic equation, but with a twist: the exponents are negative. Just as in 6.8 (the fraction/exponent/inequality combo problem), we can break down this seemingly messy situation into tractable steps:
- Factor out the quadratic expression, ignoring the negative exponents for now.
- Interpret the negative exponents to find the solutions to the equation.
Factoring the Quadratic Expression
For our factoring step, we’ll hold onto the minus signs in the exponents, but otherwise we’ll treat this like any other quadratic equation we might encounter on the GRE.
To complete the factors, we need two numbers
- whose product is -15
- whose sum is 2
Note that for a pair of numbers to have a product of -15, one of them must be negative and the other positive. Here are all of the integer possibilities:
- (-1, 15)
- (1, -15)
- (-3, 5)
- (3, -5)
Of these four integer pairs, only (-3, 5) sums to 2, which means that the correctly factored expression is
Thus, in terms of y-1, our two solutions are
Negative Exponents
Now we have to reckon with the other piece of the puzzle: negative exponents. There’s a simple rule for these:
A negative exponent is the reciprocal of the corresponding positive exponent.
To put it somewhat more formally:
In terms of problem 6.24, this means that
so we can rewrite our two solutions from the previous step as follows:
Solving for y in each case gives us
The latter solution is on the answer list as (C).
A Note on Factoring
As usual, I’ve included a list of relevant Math Review sections below. I want to point out, however, that the Math Review doesn’t cover factoring in any real detail. Instead, they encourage you to use the quadratic formula as your default method.
The trouble with this is that, for the kinds of polynomials you’ll see on the GRE, factoring is usually the faster approach; for my money, it’s also easier to remember in the middle of a four-hour exam. For an extensive tutorial on factoring methods, along with plenty of worked examples, check out Khan Academy (look for “Factoring Polynomials – Quadratic Forms”).
Math Review Reference
For more on this topic, see the following sections of the GRE Math Review:
- 2.2: Rules of Exponents (pp. 18-20)
- 2.4: Solving Quadratic Equations (pp. 22-23)