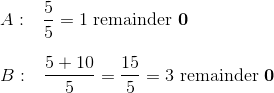This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.6: Division with Remainders

This problem is a great candidate for plugging in: once we decide on a value for n, the arithmetic is pretty simple. Without a concrete example, though, it might be hard to see the pattern that relates the two quantities.

Let’s try n = 5.

The remainders are in bold, just to emphasize the fact that this is what we’re comparing. In this case, Qty. A and Qty. B both equal 0. We can now rule out answers (A) and (B), because the two quantities are equal at least some of the time.

Now, how about n = 8?

Again, the remainders are equal. Once we’ve gotten the same result twice on a Quantitative Comparison, it’s time to step back and look for patterns. There are three basic possibilities here:

• It’s just a coincidence that the remainders were equal both times. (Unlikely!)
• There’s something about the numbers we chose — some shared property — that made the remainders equal. (Possible!)
• There something about the structure of the problem that guarantees that the remainders will be equal, no matter what n we choose. (Possible!)

In this case, the last option is correct. There’s nothing special about the n we chose; any positive integer would give the same results. Because 10 is divisible by 5, adding it to the numerator will never change the remainder. Imagine a clock with just 5 hours on it. In this illustration, it’s 1:00 right now:

But if we advance the time by 10 hours, to 11:00, the clock will look exactly the same, because we’ve gone around the clock exactly twice.

Our answer, by the way, is (C).

(Challenge question: how would the problem be different if we were comparing the remainders of n and (n + 11)? What values of n could we try to demonstrate this behavior?)

A Quick Note about Remainders

Just to clear up a point that some students find confusing: if your dividend is smaller than your divisor, the remainder is the entire dividend — not zero, and not undefined. So if we’d chosen 4 as our value for n above, we’d have gotten the following result.

If this seems counterintuitive, think of it this way: You have a bunch of friends over for dinner and plan to serve cheesecake after the meal. There are 6 people at the table, including yourself, and the cheesecake, which was store-bought, came pre-sliced into 6 neat slices. So the plan is for each person to get 6/6 = 1 slice of cheesecake, with none left over (i.e., no remainder).

But your roommate/spouse/pet, who was not aware of your plans for the cheesecake, has already eaten 2 of the slices. So when you go to the fridge to retrieve the dessert, you find that you have only 4 slices left. It’s a nice evening, so you quickly formulate a backup plan: “Let’s all go out for ice cream!” None of the cheesecake has been divided up among you and your guests, but those four slices are still there in the fridge for later. In other words,

Math Review Reference

For more on this topic, see the following section of the GRE Math Review:

• 1.1: Integers (pp. 1-2)