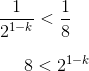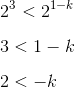This page is part of my unofficial solutions manual to the GRE Paper Practice Book (2e), a free resource available on the ETS website. They publish the questions; I explain the answers. If you haven’t worked through the Practice Book, give Section 6 a shot before reading this!

6.8: Exponents in the Denominator

This problem combines three mathematical concepts that, by themselves, tend not to cause much trouble: fractions, exponents, and inequalities. If your algebra is a bit shaky, it may help to think of this problem in terms of three basic steps:

• Get rid of the fractions, leaving 2^1-k on one side of the expression.
• Get rid of the exponents, leaving (1 – k) on one side of the expression.
• Solve for k.

To clear out those fractions, we can cross-multiply:

(Note that even though k might end up being negative, 2^1-k will be positive for any real value of k, so we don’t have to worry about sign-flipping here.)

8 is a power of 2, so we can rewrite it as 2³:

Now, remember the property of equality of exponential functions (see problem 5.16 for a refresher)? A similar property applies to inequalities, although the Math Review doesn’t mention it:

The main difference between this and the equality property is that here, the base x has to be greater than 1. Our base in this problem is 2, so we’re in the clear.

For the last step, we multiply both sides by -1 (this time, the direction of the inequality does change).

Because k (Quantity A) is less than -2 (Quantity B), the correct answer is (B).

Math Review Reference

For more on this topic, see the following sections of the GRE Math Review:

• 1.2: Fractions (pp. 3-4)
• 2.2: Rules of Exponents (pp. 18-20)
• 2.5: Solving Linear Inequalities (pp. 23-24)